Social Media Experiments and Weighted Averages

Recent criticisms of Haidt & Rausch are based on the mistaken notion that the application of a random effects model would somehow contradict their findings.

Jonathan Haidt and Zach Rausch have written an After Babel article that has been criticized by a few pundits for not using a ‘random effects’ model — including the use of weights and the production of p values and confidence intervals — similarly or identically to a meta-analysis by the psychologist Chris Ferguson, which Haidt and Rausch were criticizing.

The evidence Haidt & Rausch has provided is fine on its own: for example they showed that all the SM abstinence experiments lasting less than a week have substantially negative effect sizes (as calculated by Ferguson) while none but one of the experiments lasting 2 or more weeks do — instead the long lasting SM use reduction experiments tend to have positive effect sizes.

Some pundits seem convinced, however, that this evidence would somehow disappear with weights applied in a ‘random effects’ model such as the one used by Ferguson.

That is incorrect, as I will show.

WARNING: nothing in this article should be interpreted as an agreement that, in order to investigate the validity of some meta-analysis, one must first presume the meta-analysis to be valid and, out of infinitely many possible weight schemes, presume the one used by that meta-analysis is the only one that is legitimate.

My Criticism of Ferguson’s Meta-analytic Review

As Haidt and Rausch (H&R) note in their article, they have based their objections to Ferguson’s analysis on my own critique of Ferguson: Fundamental Flaws in Meta-Analytical Review of Social Media Experiments.

In my critique, I wrote that the design of Ferguson’s meta-analysis is fundamentally flawed and impossible to fix. Furthermore, I told H&R back in May that I do not think that Ferguson’s particular collection of experiments and composite effects sizes can be subject to a valid ‘random effects’ analysis. That is likely why H&R did not attempt any such ‘random effects’ analysis in their own article.

I’ve been doing some part-time work over the Summer for Haidt, helping with projects such as an Experimental Studies Database that, I hope, will provide a basis for an ongoing systematic review of experimental evidence relevant to SM impacts on MH. For this reason I’m now reluctant to get involved in public disputes regarding Haidt.

I will therefore focus only on showing that certain parts of my own critique, including the parts relevant to the H&R article, remain true even if one presumes that somehow the only allowed method of investigating relationships within Ferguson’s data is a random effects model.

WARNING: nothing in this article should be interpreted to mean that Ferguson’s meta-analysis is valid.

​ㅤ

Ferguson’s Model Results

Ferguson did his meta-analysis (model estimator Maximum Likelihood) using the Jamovi software and, per his communication with Zach Rausch, used solely the effect sizes and sample sizes from his online OSF table as inputs to obtain the following estimate and confidence interval:¹

0.088 (-0.018, +0.197)

I was able to precisely replicate this result, as well as other results provided by Ferguson (such as moderator and heterogeneity analysis).

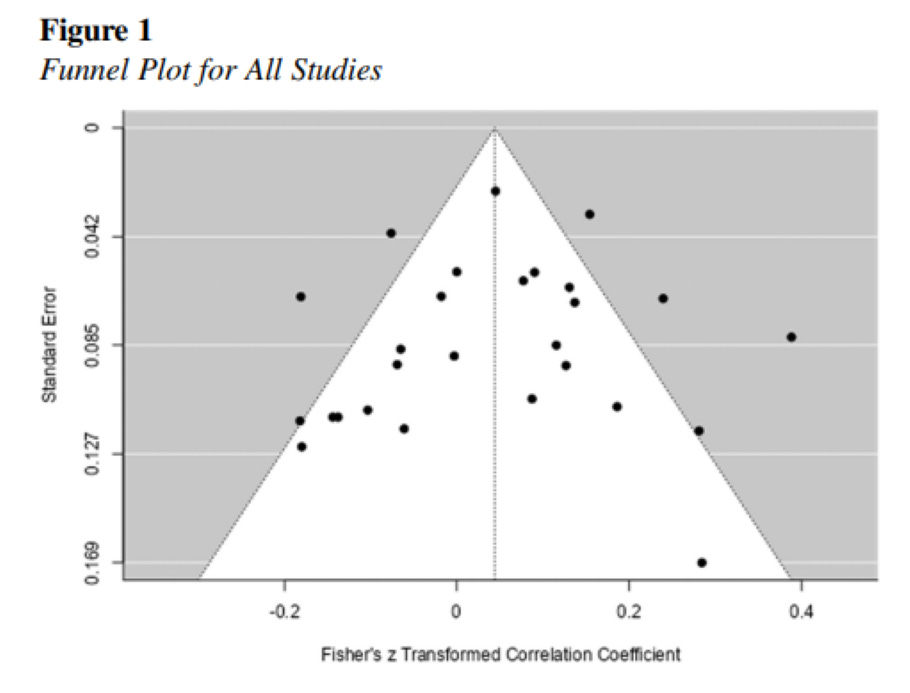
Ferguson inexplicably did not provide a Forest plot in his paper, but he did provide a Funnel plot in Figure 1, so we can compare his plot with mine:

The above is Ferguson, the below is mine:

Here is the Forest Plot (Ferguson did not include one in his meta):

Note: some of the citations are misspelled (Alcott instead of Allcott, Collins instead of Collis, Kleefeld instead of Kleefield) because I used as input Ferguson’s data table as is, without any corrections.

ㅤ

Erroneous Data

Before we discuss Ferguson’s failure to investigate certain relationships within the data, it needs to be noted that the data itself is severely erroneous: several studies were assigned indefensible effect sizes and at least three sample sizes are very wrong. Furthermore, Ferguson included several studies that violated his own criteria (and failed to include several studies that did fit his criteria).

Each one of these errors biased the analysis toward the negative, thus helping to achieve statistical insignificance.

Note: for details about these errors, see Fundamental Flaws in Meta-Analytical Review of Social Media Experiments.

In my critique, I predicted that correcting even one large error in the data — that of Lepp 2022 — would flip the result to significance. Indeed, I can now confirm that this is true: after assigning a minimal defensible effect size² of d = +0.27, the confidence interval ceases to include zero and p is below 0.05:

+0.106 (+0.002, +0.210) with p = 0.046

So Ferguson’s insignificant result is so flimsy that even a single correction of an effect size in his data can flip the result to significance.

If we fix the two erroneous effect sizes (from Lepp 2022 and Brailovskaia 2022) and the three sample size errors (from Przybylski 2021, Lepp 2022, and the Kleefield dissertation), the result moves further away from zero:

0.112 (+0.008, +0.214)

If we also exclude the two studies that violated Ferguson’s own criteria (Deters 2013 and Gajdics 2022), the result is:

0.145 (+0.048, +0.245)

Including several studies inexplicably excluded by Ferguson — each indicating that SM use is harmful — would likely more than double Ferguson’s 0.088 result.

​ㅤ

Potential Moderators

Now let us ask if, even with the above errors uncorrected, the data reveals influence of factors such as the presence of a mental health outcome or the duration of experimental intervention.

Note: I leave the data uncorrected to demonstrate that Ferguson himself could and should have easily noticed the role of important factors based even on the erroneous data he used.

Borenstein et al. 2010, in their guide A basic introduction to fixed-effect and random-effects models, warn:

The third caveat is that a random-effects meta-analysis can be misleading if the assumed random distribution for the effect sizes across studies does not hold.

Let’s first consider an example as to why lack of random distribution can be very important.

ㅤ

Why Subgroup Analysis is Important

To better understand why proper subgroup analysis can be crucial in a meta-analysis, imagine that Ferguson is working for a pharmaceutical company that manufactures a weight-loss drug X.

The company conducts numerous experimental studies: there are 20 studies that show drug X improves body image and 10 studies that provide statistically significant evidence that drug X increases suicidal ideation and conduct.

Ferguson combines the effect sizes from the 20 body image studies and the 10 suicidal conduct studies to calculate a ‘weighted average’ in a random effects model and obtains a result that indicates harm but is statistically insignificant.

A subgroup analysis would reveal that the 10 suicidal conduct studies provide statistically significant evidence of mental health harm, but Ferguson omits any hint of this when he publishes his meta-analysis.

Instead, Ferguson declares that his meta-analytic results ‘undermine’ any concerns about the effects of the weight-loss drug X on mental health and even announces publicly that his findings show that drug X has “no impacts on mental health”.

Such conduct would be wrong, scientifically as well as ethically. Proper subgroup analysis is a necessity, especially when public health is at risk.

ㅤ

Mental Health Measures

I criticized Ferguson for refusing to analyze mental health outcomes such as depression and anxiety, since these are the MH disorders that scholars like Haidt and Twenge maintain have been rising among youth due to the spread of smartphones and social media use. Ferguson instead created ill-defined composites of general ‘well-being’ outcomes that obscured well-defined depression and anxiety measures.

To demonstrate the relevance of MH outcomes³ to the analysis, I noted:

[F]or the SM use reduction field experiments that included a MH outcome, the average Ferguson effect size is d = +0.27, indicating MH benefits; but for the SM use reduction field experiments that did not include a MH outcome, the average Ferguson effect size is d = -0.12, indicating ‘well-being’ harm.⁴

So what happens if we use Ferguson’s random effects model to investigate the MH/WB split?

Note: The MH label here signifies the study measured depression or anxiety outcome (WB label means it did not).

11 MH Studies: d = +0.22 (+0.10, +0.39)

16 WB Studies: d = -0.03 (-0.15, +0.09)

So we can see the application of the weights does not negate the problem.

And if we request Jamovi to provide a moderator analysis on the MH/WB split:

MH Moderator: d = 0.27 (+0.08, +0.46), Z = 2.84, p = 0.005

So the weighted averages come out similar to the plain averages, a moderator analysis confirms, within Ferguson’s model, the relevance of the presence of a MH measure to the outcome, and the SM use reduction studies that included MH outcome produce a robust evidence of beneficial effects (within Ferguson’s model).

ㅤ

Duration of Intervention

I also criticized Ferguson for including very short SM abstinence experiments without disclosing the fact that scholars like Haidt and Twenge predict withdrawal symptoms, the opposite of well-being improvements. Ferguson used the outcomes from these short abstinence studies to weaken evidence of benefits in longer SM reduction studies within his flawed meta-analytic design and then announced that the meta-analytic result undermines theories of Haidt and Twenge.

Furthermore, I demonstrated that Ferguson’s data is concordant with the theories of withdrawal symptoms if we take into account duration of the field experiments: (plain averages) d = -0.18 for single day abstinence, d = +0.02 for 1-week reductions, and d = +0.20 for multi-week reductions.⁵

So does this evidence disappear if we use weighted averages according to Ferguson’s random effects model? The results are as follows:

3x single day SM abstinence: d = -0.17 (-0.29, -0.05)

If we include the 5 day abstinence experiment in Mitev 2021:

4x less than 1w SM abstinence: d = -0.17 (-0.28, -0.05)

Now compare with longer experiments:

7x 1w SM reductions: d = +0.08 (-0.20, +0.36)

The wide CI indicates great heterogeneity, which is likely explained by the types of outcomes measured in these experiments — did the study authors focus on momentary moods subject to withdrawal symptoms or did they focus on mental health outcomes like depression?

10x 2w or longer SM reductions: d = +0.16 (+0.06, +0.26)

In the even longer SM reduction studies the heterogeneity is far lesser, indicating that any traces of withdrawal symptoms are gone, no matter the focus of the studies.

So the the evidence remains when we use weighted averages.

Finally, let’s consider all the 17 experiments that lasted at least 1 week:

17x 1 week or longer: +0.15 (+0.02, +0.28)

So simply removing the lab studies and the 4 very short (less than a week) abstinence experiments increases the result to d = 0.15 — and that’s before any data corrections.

Ferguson has given no hint in his paper that duration of the experiments is a relevant factor. Had he shown how the results differ based on the length of the experiments, and had he admitted that scholars like Haidt and Twenge predict withdrawal symptoms in short abstinence experiments, his conclusion that his result undermines the theories of Haidt and Twenge would be recognized as unsound.

Note: Ferguson has also publicly declared that his analysis “finds that reducing social media time has NO impact on mental health.” This requires no analysis — it is just plain misinterpretation of statistical insignificance as proof of no effect.

ㅤ

Sample Size

I also mentioned in my critique that sample size appears to be substantial predictor of the effect size: “out of the 27 studies, the 13 higher-powered experiments produced a far greater average impact (d = 0.15) than the 13 lower-powered studies (d = 0.01).”

So does the disparity disappear if we use weighted averages?

As we can see the answer is no:

13 higher-powered experiments: d = +0.17 (+0.02, +0.30)

13 lower-powered experiments: d = 0 (-0.16, +0.16)

Borenstein et al. elaborate:

The third caveat is that a random-effects meta-analysis can be misleading if the assumed random distribution for the effect sizes across studies does not hold. A particularly important departure from this occurs when there is a strong relationship between the effect estimates from the various studies and their variances, i.e. when the results of larger studies are systematically different from results of smaller studies. This is the pattern often associated with publication bias, but could in fact be due to several other causes.

In the case of Ferguson's collection of studies, the question is why the studies with lower sample sizes produced much lower effect sizes.

ㅤ

Discussion​

It is important to differentiate between evidence contradicting Ferguson’s assertions and evidence that SM reductions will improve mental health.

Ferguson’s effect sizes are ill-defined composites of general ‘well-being’ outcomes that obscured depression and anxiety outcomes.

Ferguson did not reveal how he calculated the effect size for each of the studies, what were the effect sizes of the individual WB components (such as depression or anxiety), or even which aspects of WB outcomes he chose to include in his composite calculations.

I think that it was unfortunate for Haidt and Rausch to start their ‘Case for Causality’ series with Ferguson’s paper, since Ferguson’s review is of so low a quality and so erroneous that its meta-analytic framework should be used solely to demonstrate the lack of its own validity. It is therefore best to keep responses to his paper separate from any serious investigations of causality.

The poor quality of Ferguson’s data is also why I think it was a mistake for Haidt to use Ferguson’s effect sizes as evidence of SM reduction impacts on MH.

Was it factually wrong to do? No, the effect sizes are no doubt somewhat related to MH outcomes.

The association, however, is so muzzled that any evidence based on Ferguson’s ill-defined, undisclosed and problematic effect size methodology should be automatically judged as inherently weak.

Simply put, Ferguson’s review and data are of such a low quality that they are best kept entirely separate from any serious investigations of experimental evidence examining SM impacts on MH.

ㅤ

Conclusion

Even if we ignore the invalidity of Ferguson’s meta-analysis and the errors in his data, previous criticisms of Ferguson based on plain averages of his effect sizes are not weakened when random-effects model weights are applied instead.

ㅤ

Appendix:

Let me briefly explain some of the reasons Ferguson's meta-analysis should be considered invalid.

1) The resulting 'estimate' is meaningless as it is some weighted average of incompatible effects, such as:

• The effect on self-esteem of viewing own Instagram for 5 minutes.

• The effect of one-day smartphone abstinence in school on momentary moods such as feeling bored or irritated.

• The effect of increasing the frequency of FB status updates for one week on feelings of loneliness.

• The effect of reducing all SM by half for 3 weeks on a validated measure of depression.

One could go on and on, but it is unclear which of the many aspects of 'well-being' were included in which of the composite effect sizes, as Ferguson did not reveal this information.

2) There is no reason to think the resulting 'estimate' is actually an estimate of anything independent of the selected studies, nor that there is any way to validate the estimate, even if one had unlimited information. Compare with, say, the example of a meta-analysis in Borenstein et al. 2010, where the mean aptitude score of freshmen students in California is being estimated from various samples within different colleges: here what is being estimated is well-defined and exists in theory independent of any particular collection of sampling studies — and its precise value could be determined (if all students in the state were tested).

3) It is invalid to conduct a meta-analysis where you ignore the role of independent factors, such as duration of treatment or the amount of medication administered. When such factors are relevant, one needs to conduct a subgroup analysis or a meta-regression. As Borenstein at al. wrote: "The third caveat is that a random-effects meta-analysis can be misleading if the assumed random distribution for the effect sizes across studies does not hold."

4) Ferguson misapplies his model as if it was an accurate framework for the evaluation of theories proposed by Haidt & Twenge, but this is false due the consequent interpretation of withdrawal effects in short abstinence experiments as evidence that Haidt & Twenge are wrong, even though they predicted these results.

I suggest Borenstein et al. 2010 and Hodges & Clayton 2011 as further reading.

Note that it is crucial to distinguish between proper calculation of a model and the actual validity of the model, which always depends on its interpretation.

For example, one can calculate ‘linear regression’ with pretty much any numerical data, but this does not validate any model of reality. If you apply such a model to a U-shaped relationship between weight and some aspect of health and conclude there is no relationship because the linear correlation is nearly zero, you are concluding falsehoods because your model of reality is invalid.

If you apply a linear model to yearly data of U.S. eagle population, you might get a very close ‘fit’ (such as r = 0.914), but presuming that this is a valid model of reality can lead you nonsense such as that there were a negative 2000 eagles in 1960.

Ferguson explicitly uses his random-effects model result as a test of “causal claims by some scholars (e.g., Haidt, 2020; Twenge, 2020) that reductions in social media time would improve adolescent mental health” — in other words Ferguson posits his model as a valid model of reality.

That this is preposterous is given already by the fact that in Ferguson’s model the evidence of withdrawal symptoms — predicted by scholars like Haidt and Twenge — in very short abstinence experiments is used to ‘prove’ that Haidt and Twenge are wrong. This is akin to Ferguson constructing a model in which withdrawal symptoms during initial stages of heroin abstinence are interpreted as proof that heroin is good and heroin abstinence is harmful.

The problems with Ferguson’s model, however, go much deeper. Even if we removed the short abstinence experiments from the data, the severe methodological heterogeneity of the remaining experiments and, especially, the fuzzy potpourri of ‘composite’ effect sizes invented by Ferguson, render the resulting ‘estimate’ practically meaningless.

1. Ferguson converted his Cohen’s d effects into r correclations and then back again to d. There are some technical issues regarding such conversions, plus it seems the output in Ferguson’s analysis was Fisher’s z, not r. These issues are minor compared to the many major flaws in Ferguson’s analysis.

2. In Lepp, a SM lab exposure experiment, there is no valid control group or condition, which is similar to Gajdics, where it seems Ferguson simply compared the before and after group means to calculate Cohen’s d. The situation is complicated in Lepp by the availability of outcome measures at mid-point of the intervention; using repeated ANOVA would result in an effect size of d = 0.45, but the effect size from the plain change score is d = 0.27. I therefore use the smaller value, that is the weaker effect size of harmful SM impact.

3. In this analysis I mean by MH outcomes specifically depression and anxiety, since the 27 studies did not include indicators of any other mental health disorders.

4. Deters is actually not a SM use reduction study, or even a SM time manipulation experiment (as required by Ferguson’s stated criteria), but I leave it in as one of the errors, in order to go strictly by the data interpretation used by Ferguson.

5. I counted Mitev 2021, an abstinence experiment that lasted 5 days, as a 1 week study.